The discovery of the Higgs boson in 2012 is an epoch-making event in particle physics research. It plays a key role in the "Standard Model" of particle physics. It brings mass to elementary particles through a mysterious symmetry breaking mechanism. It is closely related to the unpredictable quantum vacuum and is also considered to be important in the very early days of the evolution of the universe. effect. On the tenth anniversary of the discovery of the Higgs boson, this article will describe the theoretical background, particle characteristics, experimental detection, research status and prospects of the Higgs boson from the perspective of popular science, and uncover the Higgs boson to understand its past, present and future.

1 Introduction

Particle physics studies the most basic components of the material world and their interaction laws, explores the microscopic "small universe" among elementary particles, and pursues the understanding of a series of fundamental questions: Is there an ultimate indivisible smallest unit of matter? What are the interactions between elementary particles? What is the root cause of the interaction? What is the nature of time and space?

From the atomic theory in ancient Greece, to modern quantum mechanics, to the standard model of particle physics based on quantum field theory, human beings have gradually established a mature understanding of the microscopic particle world from philosophy to science, combining theory and a large number of experimental discoveries. describe. The last experimentally confirmed elementary particle in the Standard Model was the Higgs boson. It is often dubbed the "God Particle" in the media, and its corresponding Higgs field is considered to be the source of the mass of elementary particles and plays a pivotal role. There are still many major scientific issues to be explored in particle physics, such as the nature of dark matter, the asymmetry of positive and negative matter in the universe, the mass of neutrinos, and so on.

The Higgs boson was discovered in 2012 [1, 2], and Peter Higgs and Francois Engler, among the theorists who directly contributed to the particle hypothesis [3-5], won the 2013 Nobel Prize in Physics. The research on the Higgs particle is an important direction in particle physics, and has since entered the measurement mode from the search mode. Scientists hope to examine this new thing buried deep in the microscopic world through more experimental data, and look forward to discovering its connection with new physics.

2022 is the 10th anniversary of the discovery of the Higgs boson. This article will start from the following aspects: theoretical background, characteristics of the Higgs boson, experimental detection of the Higgs particle, and the results of Higgs physics research. Current status and outlook.

2. Theoretical background

On July 4, 2012, amidst the applause and cheers of his peers, physicist Rolf Heuer, then director of CERN, officially announced that after decades of exploration, thousands of scientists have achieved the results of the Large Hadron Collider. The Higgs boson was discovered on the LHC. The Higgs boson is the last piece of the puzzle for physicists in their quest to understand the Standard Model of particle physics. With the Higgs boson, the Standard Model of particle physics is complete.

Particle physics holds that all observed matter is composed of elementary particles. The Standard Model holds that there are three charged leptons in the world: electrons, muons, and tau leptons, which participate in electromagnetic and weak interactions. There are three kinds of uncharged neutrinos in the world, and they only participate in weak interactions. Protons and neutrons in atomic nuclei are not elementary particles, they are made of quarks. Quarks are fundamental particles, and they cannot be further divided. The Standard Model holds that there are six types of quarks in the world (up, down, strange, charm, bottom, and top) that participate in electromagnetic, weak, and strong interactions. Quantum field theory holds that the interaction of matter is transmitted through the medium boson: the electromagnetic interaction is transmitted through the photon. We know that according to the wave-particle duality of quantum mechanics, electromagnetic waves have the properties of particles, and the corresponding particles are photons. Weak interactions, such as the beta decay of nucleons, are transmitted by W and Z bosons. The strong interaction is transmitted through gluons. With the discovery of the top quark by the Fermi National Laboratory in the United States in 1995, all of the above elementary particles have been discovered.

Among the above-mentioned interactions, why the weak interaction is so "weak" is an important question in the history of the development of particle physics. For example, as an unstable particle, the muon has a relatively very long lifetime. The reason is that the decay of the muon comes from the weak interaction, which has a low strength, so the decay is not easy to occur. The earliest theoretical interpretation of the weak interaction is Fermi's "four-fermion" theory, which can explain the phenomenon of beta decay in the low-energy region, but the theory becomes inconsistent in the high-energy region. Moreover, this theory is completely different in form from the quantum electrodynamics of Feynman, Schwinger, and Shinichiro Tomonaga, making theoretical physicists question whether there is a more unified theory to describe the fundamental interaction.

Quantum electrodynamics describes electromagnetic interactions in which quantized photon fields convey the interactions. The gauge transformation of the electromagnetic potential endows the theory with the so-called U(1) gauge symmetry. Mathematically, U(1) symmetry is equivalent to complex multiplication on the unit circle. The deep idea of gauge symmetry is used to study other fundamental interactions. Gell-Mann proposed new elementary particles, quarks, which are the building blocks of nucleons. Gell-Mann argued that the quark model could be used to describe the spectrum of nucleons if there was a new physical degree of freedom for quarks, namely three "colors." Quarks participate in strong interactions, which in Gell-Mann's theory are transmitted via gluons. Yang-Mills theory, that is, non-Abelian gauge theory, was used to describe the strong interaction and developed into quantum chromodynamics. The three colors correspond to the mathematical SU(3) gauge symmetry.

The "four-fermion" theory is different from both quantum electrodynamics and quantum chromodynamics. In this theory, there are no intermediary particles for propagating interactions, and there is no gauge symmetry. The coupling constants of quantum electrodynamics and chromodynamics are dimensionless, but the coupling constants of the "four-fermion" theory are negative powers of energy. This means that this theory is not renormalizable, will be inconsistent in high-energy regions, and needs to be replaced by a more general theory. One attempt is to use Yang-Mills theory to describe the weak interaction, and introduce a new gauge boson to describe the weak interaction. However, the weak interaction is a very weak short-range force, and the gauge bosons that transmit the weak interaction must have mass, which is different from quantum electrodynamics and chromodynamics. The propagator of quantum electrodynamics is a massless photon, and the propagator of quantum chromodynamics is a massless gluon. It is difficult to obtain a self-consistent gauge theory by adding gauge boson mass directly into Yang-Mills theory.

To construct weak interaction models within the framework of Yang-Mills theory, completely new physical ideas are essential. The winning ideas here are spontaneous symmetry breaking and the Higgs mechanism. Glashow, Weinberg, and Salam respectively proposed the idea of electroweak unification, unifying the electromagnetic interaction and weak interaction in the Yang-Mills theoretical framework. Breaking this unity directly, introducing gauge boson masses, is, as mentioned earlier, theoretically very difficult. Here, the self-consistent modeling approach is to introduce spontaneous symmetry breaking. That is to say, in the unified Yang-Mills theory, the interaction does not directly break the gauge symmetry, but the ground state of the quantum field breaks the gauge symmetry.

Spontaneous symmetry breaking is actually not uncommon in our macroscopic world. The ground state of the magnet at room temperature has spontaneous magnetization. A bar magnet has an N pole at one end and an S pole at the other end. The polarity of the two ends destroys the symmetry of the bar magnet. Note that the electromagnetic interaction itself does not break the symmetry, but there are two ground states of the bar magnet, and the system chooses one of the ground states to break the symmetry spontaneously. In quantum field theory, similar to the magnet model, a so-called scalar field may also have multiple ground states, then the ground state selection of the physical system spontaneously breaks the symmetry. The scalar field to be introduced here is the famous Higgs field (Figure 1)[6].

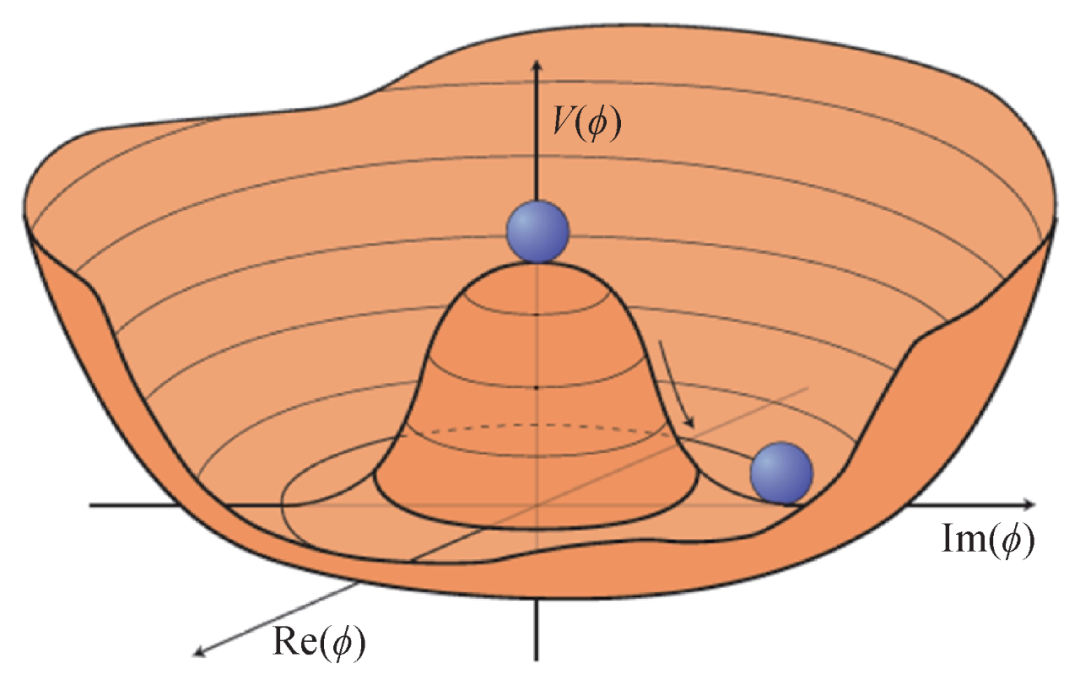
Fig.1 Potential energy form of Higgs complex scalar field[6]

In general, spontaneous symmetry breaking in field theories produces massless scalar particles due to the so-called Goldstone mechanism. Although the particle physics model constructed in this way has introduced the electromagnetic interaction and weak interaction into the framework of Yang-Mills theory, massless scalar particles have never been found experimentally, which is still a theoretical problem. The Higgs mechanism finally solves this conundrum: the original massless gauge boson absorption "eats" the massless scalar particles produced by spontaneous symmetry breaking. In this way, the massless scalar particle is eliminated, and at the same time, the mass of the gauge boson is given to the weak interaction, which shows that the weak interaction is a weak short-range force. From a theoretical point of view, the Higgs mechanism is a key step in the unification of electroweak interactions.

In the specific model construction, how to choose the correct symmetry and breaking method is very important for predicting the type and interaction of new particles. Weinberg and Salam chose the SU(2)×U(1) symmetry group and a pair of complex Higgs fields. This ground state of the complex Higgs particle field will break the SU(2)×U(1) symmetry, and the remaining U(1) symmetry corresponds to the electromagnetic interaction. The three broken symmetries, due to the Higgs mechanism, lead to the production of three gauge bosons with mass, namely W+, W- and Z bosons. These three particles convey short-range weak interactions. The three physical degrees of freedom in a pair of complex Higgs fields are eaten by W and Z, and the only remaining physical degree of freedom corresponds to the excited state of quantum field theory, which is the so-called "God particle" - Higgs particle.

The Higgs field is also coupled with the matter fermion field (such as electrons, muons, tau leptons, and quarks) through the Yukawa mechanism. In the Higgs mechanism, the ground state of the Higgs field becomes equivalent to the mass parameters of these matter particles. In layman's terms, the Higgs field gives elementary particles their mass. Weinberg and Salam's model of electroweak unification and spontaneous symmetry breaking, together with quantum chromodynamics, which describes the strong interactions, constitute the standard model of particle physics.

Gradually, experimental physicists probed and discovered all the fundamental particles in the Standard Model except the Higgs particle. For decades, only the Higgs boson eluded all attempts to detect it -- until July 4, 2012, when the Higgs boson was officially announced at CERN in Geneva, the final piece of the Standard Model The puzzle is complete. This is the first elementary particle with zero spin in nature.

The Standard Model is considered complete, but many questions are far from being answered.

3. Characteristics of the Higgs particle

As an elementary particle, the Higgs particle also has its unique quantum parameters. As the only scalar boson among the fundamental particles in nature, according to the prediction of the standard model, its spin is 0 and its parity is positive. The Higgs mechanism of the Standard Model not only endows the W and Z gauge bosons with mass, but also determines their interactions with other elementary particles in the Standard Model. As a boson, the Higgs is quite active and can interact with fermions and other gauge bosons. Specifically, the coupling strength of the interaction between the Higgs particle and the fermion is proportional to the mass of the fermion, so in the standard model, the Higgs particle has the strongest interaction with the top quark with the largest mass, and the interaction with the electron The coupling strength is the weakest. In the Standard Model, neutrinos have no mass, so the Higgs particle does not interact with neutrinos. The Higgs-fermion interaction is also known as Yukawa coupling, and it is from this interaction that fermions gain mass. There are gauge interactions between the Higgs particle and the massed W and Z bosons, but no interaction with the massless photons and gluons. In addition, the Higgs interacts with itself, including three-Higgs and four-Higgs couplings, known as Higgs self-interactions.

It is worth mentioning that almost all the physical properties of the Higgs particle are predicted by theory, except that its mass is a free parameter that needs to be measured by experiments. And precisely because of the uncertainty of the mass of the Higgs particle, experimentalists have spent a lot of time and energy looking for this particle, because they need to look for possible Higgs boson signals in the unknown mass range like a needle in a haystack . Although the mass of the Higgs particle is a free parameter, it is related to the self-interaction coupling constant of the Higgs particle. As long as one of the two can be determined, the other parameter will also be determined. Another important quantum parameter related to the Higgs mass is its mass width, or decay width. According to the theoretical prediction, once the mass is determined, its mass width is also determined, and the mass width determines the life of the particle. The Higgs particle, discovered in 2012, has a mass of about 125 GeV, which is equivalent to 130 times the mass of a proton. It is the second-heaviest particle in the standard model of elementary particles after the top quark.

The importance of the Higgs particle is not only that the Higgs mechanism behind it is the origin of the mass of elementary particles, but also that it has a profound connection with new physics and cosmology beyond the standard model. A classic example is the interaction between vector bosons. According to the prediction of the standard model, the scattering process can occur between vector bosons, and the scattering amplitude includes the coupling between Higgs particles and vector bosons. Calculations show that this scattering amplitude is proportional to the square of the center-of-mass energy of the incident particle pair if no Higgs particle is involved. This means that in the absence of the Higgs particle, this scattering amplitude will diverge at high energies, which means that new physical phenomena will emerge. Although the appearance of the Higgs particle can avoid this divergence, this is only one of many possibilities, and there is no reason to think that no other new physics beyond the standard model will participate in the scattering process of this vector boson. As mentioned earlier, the Higgs particle is an important participant in the spontaneous symmetry breaking of weak interactions, a phase transition process that occurred very early in the evolution of the universe. The self-interaction of the Higgs particle determines the potential energy of the Higgs field, and this potential energy function also determines the phase transition process of breaking the electroweak symmetry, which means that the Higgs particle has a profound connection with the evolution of the universe.

The Higgs boson's interactions with other particles point the way for physicists to search for the Higgs experimentally. Depending on how it interacts with the rest of the particles, the Higgs can be created in high-energy colliders, such as the LHC. The LHC can accelerate protons to extremely high energies, and the energy of the proton-proton center-of-mass system can reach 14 TeV. The production mode of the Higgs particle on the LHC is relatively complicated. Calculations show that the main production mode is the gluon-gluon fusion process, accounting for about 80% of the cross-section. The other production modes are boson fusion and boson fusion in sequence. adjoint and top quark pair accompaniment production process. In fact, the total production cross-section of Higgs particles at the LHC is considerable, so the LHC is actually a "Higgs boson factory".

Although a large number of Higgs bosons can be produced in the LHC, the Higgs particle is so short-lived that it decays instantly after creation. Like radioactive decay in nature, one particle decays to produce other products. Because the Higgs particle is very active, its decay mechanism is quite complicated. Physicists use the probability of decay, or decay branching ratio, to measure how easily a particle undergoes a particular decay process. The decay branching ratio of the Higgs particle depends on several corresponding physical parameters, such as the mass of the Higgs particle, the mass of the final decay state particle, and the coupling strength between the Higgs particle and the final decay state particle. Once the mass of the Higgs particle is determined, the cross-sections of its various production processes at the LHC and the branching ratios of each final decay state are correspondingly determined (Fig. 2)[7]. For example, for the Higgs boson with a mass of 125 GeV, its main decay final state is two bottom quarks, with a branch ratio of about 56%, followed by the decay to two W bosons (23%), and other The branching ratio of each boson or fermion final state is different.

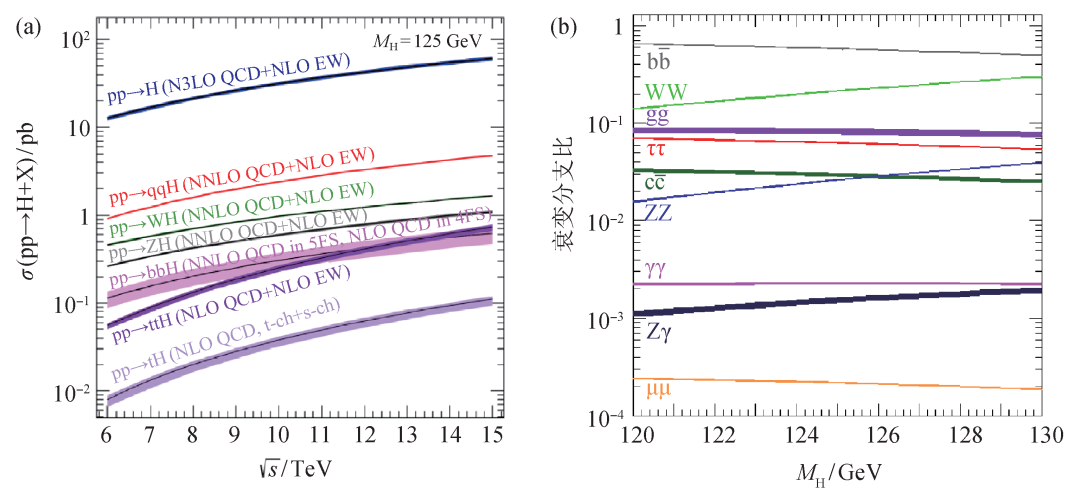
Fig. 2 The generation cross-section (a) and decay branch ratio (b) of the Higgs boson on the proton-proton collider[7]

In fact, experimentally observing the Higgs signal is an extremely complex and challenging task. Since the Higgs particle has different modes of production and decay, the two can be combined arbitrarily, which means there are many ways to look for the Higgs signal. The higher the generated cross-section and the larger the decay branching ratio, it means that the more Higgs particles can be observed, and vice versa, as shown in Figure 2. In addition, the final decay state of the Higgs particle needs to be detected by experimental instruments, and the detection methods and difficulty levels of different final state particles also vary greatly. For example, it is more difficult to detect the final state of the tetralepton, whose decay branch ratio is much smaller than that of the top quark pair whose decay branch ratio is much smaller. What makes the task of finding the Higgs even more difficult is that the LHC is not only a Higgs factory, it also produces other physical processes with a larger amount of data, such as the top quark production process, the vector boson production process, etc., and The data detected by the experimental instrument is a mixture of these different physical processes. It is not an exaggeration to describe it as "finding a needle in a haystack" to find the signal of the Higgs particle from massive amounts of data.

4. Experimental detection

As mentioned above, the experimental phenomenon of the Higgs particle is very rare, and it is necessary to search for it from a large amount of noise like "finding a needle in a haystack". In addition, its mass cannot be predicted with certainty. These factors have brought great difficulties to the search work . In fact, it took nearly half a century from the proposal of the Higgs mechanism and the Higgs particle (1964) to its discovery (2012), which also reflects the arduousness of experimental detection from the side.

Experimentally, scientists use particle accelerators to accelerate common and easily accessible particles (such as electrons and protons) to very high energies, and then bombard the target material (target experiment), or collide with another beam of high-energy particles (collider experiment) ), resulting in the interaction of the microscopic particle world. As long as the center-of-mass energy is sufficient and the initial conditions of the interaction are appropriate, it is possible to produce considerable microscopic phenomena (ie, signal processes) that scientists are interested in. Of course, unstable particles such as the Higgs boson decay almost immediately, and the final observed experimental final states actually consist of relatively long-lived particles or phenomena such as photons, electrons, muons, tau leptons, and Quantum Chromodynamics Jetting, etc. It's just that such a seemingly ordinary final state of the experiment contains traces of the signal we are looking for. Probing these experimental final states and performing data analysis can yield physical results related to the signaling process. Several key links in the experimental detection are described below.

First of all, the particle accelerator must be able to accelerate the particles participating in the reaction to sufficient energy. Scientists usually use a strong electric field to accelerate charged particles. The length of a small electron accelerator that produces medical X-rays is on the order of meters. To touch the electroweak physical energy scale where the Higgs boson is located, the length of a linear accelerator must be ten kilometers. order of magnitude. If only a small part of the energy of the particles participating in the reaction is converted into the mass of the target particle, the actual acceleration energy needs to be higher and the acceleration length needs to be longer. Under suitable conditions, a circular accelerator is often used. Particles are cyclically accelerated and stored in the circle, waiting for the opportunity to participate in the interaction between particles. The LHC is currently the largest circular accelerator with a circumference of 27 km. Such a giant facility requires the combined efforts of the whole world, and it incorporates not only human intelligence, but also various cutting-edge technologies, such as superconducting radio frequency cavities for acceleration, superconducting magnets for deflection and alignment, and superconducting magnets for control measurements. Fast radiation-resistant electronic systems, etc.

Second, an extremely large number of repeated experiments is required to probe such a rare phenomenon as the Higgs boson. We know that the observations in the microcosm are described by a certain statistical distribution. Only by accurately measuring these distributions experimentally can we explore the deep physics behind them, and it is obvious that repeated experiments with a large number of statistics are required to accurately obtain the full picture of the distribution. In addition, the reaction in the microscopic world is very complicated. For example, at the LHC, high-energy proton-proton collisions produce a "kaleidoscope", and each "flower" corresponds to a reaction process, with different occurrence rates. The occurrence of a reaction process involving the Higgs boson is extremely rare, as low as one Higgs boson for every ten billion proton-proton interactions. It is precisely for these reasons that the accelerator must be able to trigger as many reactions as possible within a limited time (usually several years) (the corresponding experimental term is called integral brightness), and at the same time, the huge facility must be stable enough to avoid error.

In the end, physical results can only be obtained by relying on high-precision detection and superb data analysis. As mentioned earlier, after a large number of repeated experiments, there may be traces of signals in the final state of very few experiments. Scientists rely on large but precise detectors to fully capture the information of the final state. Target particles such as the Higgs boson are born at the zero point of the experimental reaction time and coordinates, but they are fleeting, and the final decay product secondary particles are submerged in the final state of the experiment with hundreds of particles at every turn. Therefore, the detector must be able to track each final particle and accurately measure its path, energy, type, etc., and finally we can use this information to spy on what happened to the zero point (the term is called "reconstruction"). Figure 3 shows a detection by the ATLAS experiment of the Higgs particle decaying into the final state of the double muon experiment. The overall scientific goal of Tanwei Zhizhu makes the accuracy of these measurements extremely strict, and a series of advanced detection technologies were born and developed, many of which were later widely used in the national economy and people's livelihood, such as medical imaging, earth exploration, radiation detection, etc. . A large statistical set of experimental final states is multiplied by a large number of detector information corresponding to each final state to form a truly large data set. Scientists carefully carry out big data analysis, compare simulated data with real data, apply correction factors from detectors and theoretical calculations, and cleverly use physical laws to design screening conditions to suppress noise and improve the significance of signal detection. After repeated tempering of data analysis, reliable physical conclusions and convincing error analysis are finally given.

Fig. 3 The image display of a Higgs particle decaying into the final state of the double muon experiment detected by the ATLAS experiment on the LHC. The red track is the muon, and part of the detector structure is shown in the picture (picture source: CERN)

Due to limited space, a more in-depth introduction to experimental detection cannot be carried out, but the author hopes that the above description can help readers grasp the grand and subtle aspects of experimental detection in a general direction. After discussing these basic links, the following briefly describes the exploration process of the Higgs particle.

The starting point of truly systematic phenomenological discussion and experimental search for the Higgs particle can be roughly traced back to around 1975. At that time, through the analysis of low-energy nuclear physics data and the use of low-energy hadron collisions, scientists searched for the Higgs boson in the range of MeV and GeV, but obviously did not find any sign of its existence, so It is deduced that its quality should be above this energy range.

Time came to the 1990s in the era of large colliders. Scientists focused on the Large Electron Positron Collider (LEP) at CERN and the Proton-Antiproton Collider ( Tevatron to find the Higgs boson. The LEP ran until the millennium and then shut down to be converted into the LHC, while the Tevatron ran until 2011. No sign of the Higgs boson was found on the LEP, giving a lower mass limit of 114 GeV, and the data analysis on the Tevatron did not find it until 2011, excluding the range of 156-177 GeV. Considering that the Higgs boson was eventually found to have a mass of 125 GeV, it can be said that both attempts were close, but unlucky due to historical accident. LEP is limited by collision energy, and Tevatron is limited by statistics.

It is worth mentioning that phenomenological research is very important for finding the Higgs boson. Considering that the standard model is a renormalizable theory based on quantum field theory, it determines that there is an intrinsic relationship between the quality of the Higgs boson and many other physical quantities in the electroweak theory. Accurate measurement of these physical quantities (such as W boson Die quality, etc.) can indirectly limit the quality of the Higgs boson. On the eve of the discovery of the Higgs boson, such studies gave the most promising mass range of 120-130 GeV.

The discovery of the Higgs boson was fixed on July 4, 2012. The large-scale international cooperation experiment ATLAS and CMS on the LHC jointly announced the discovery of a suspected Higgs boson particle with a high statistical confidence. It is found that the particle mainly uses the Higgs boson with the highest detection sensitivity to decay to the final state of double Z boson, two photon and double W boson. Take the final decay of the double Z boson to 4 charged lepton final states as an example, there are only a handful of Higgs bosons actually measured, but the signal-to-noise ratio of the final state is very good, so it is statistically very important; these The signal was found in a data set nearly 1013 times as noisy as its own! In the field of particle physics experiments, the discovery of new particles is often expressed as: the real data rejects the hypothesis test that there is no signal at a significance level of several times the Gaussian standard deviation. The 2012 discovery was statistically significant at 5 times the standard deviation in a single experiment, which is equivalent to saying that there is a one in a million chance that this new particle does not exist.

This major discovery is of epoch-making significance. It helps fill in the last piece of the puzzle of the Standard Model, making the electroweak unification of the Standard Model truly complete, and the mass of elementary particles has a real theoretical source. Initial studies have found that this new particle is basically consistent with the long-awaited Higgs boson, but its true nature needs to be accurately tested with larger statistical data.

5. Outlook

The discovery of the Higgs boson is a milestone. After 2012, the era of Higgs physics has come naturally: such a new and mysterious "old" thing deserves to be carefully examined, to study its particle intrinsic properties, to study its Coupling with other elementary particles, studying the self-consistency of the Higgs mechanism behind it (such as the double boson scattering process), and studying its connection with new physics (such as dark matter), etc. Higgs physics research has become a core direction of current particle physics. From the 8 TeV collision centroid energy in 2012, the proton-proton collision energy of LHC has continued to increase to 13-13.6 TeV, creating a new world record. Today, ten years later, the number of Higgs particles obtained has increased by nearly 15 times compared with 2012. Scientists have successively verified its scalar particle characteristics, and its relationship with a series of elementary particles (top quark, bottom quark, Z boson) ions, W bosons, Tau leptons, muons), and improve the measurement accuracy of some major Higgs processes to 10%[8,9].

Scientists have largely agreed that the Higgs boson is indeed the particle required by the Standard Model. The future of Higgs physics research may be more diverse: continue to explore the observable Higgs process in the LHC experiment, and accurately test the predictions of the Standard Model; make full use of LHC experimental data to explore rare Higgs physics processes, such as the Higgs Bose Coupling, self-coupling, and invisible decay of fermions with lighter fermions, etc., in order to discover anomalies and reveal their relationship with new physical phenomena; explore the role of the Higgs boson in the evolution of the universe and the vacuum electroweak phase transition role, explore possible complementary experimental observations, and so on. Now is the first decade of Higgs physics, and hopefully the second and third will bring new and exciting discoveries.

references

[1] ATLAS Collaboration. Phys. Lett. B, 2012, 716: 1

[2] CMS Collaboration. Phys. Lett. B, 2012, 716: 30

[3] Englert F, Brout R. Phys. Rev. Lett., 1964, 13:321

[4] Higgs P W. Phys. Rev. Lett., 1964, 13:508

[5] Guralnik GS, Hagen CR, Kibble TW B. Phys. Rev. Lett., 1964, 13: 585

[6] Ellis J, Gaillard MK, Nanopoulos D V. 2012, arXiv:1201.6045

[7] LHC Higgs Cross-section Working Group. 2016, arXiv: 1610.07922

[8] ATLAS Collaboration. Nature, 2022, 607 (7917): 52

[9] CMS Collaboration. Nature, 2022, 607 (7917): 60

(The authors Wu Yusheng and Xu Lailin are from the Particle Science and Technology Research Center and the State Key Laboratory of Nuclear Detection and Nuclear Electronics, University of Science and Technology of China, and Zhang Yang is from the Interdisciplinary Theoretical Research Center and Peng Huanwu High Energy Basic Theory Research Center of the University of Science and Technology of China. The original title " Talking about the Higgs particle", this article first appeared in the 11th issue of "Physics" in 2022. Surging Technology is authorized to repost.)